Voronoi-Diagramme berechnen
Bei der Berechnung von Voronoi-Diagrammen steht man vor der Entscheidung entweder einen einfachen Algorithmus zu verwenden oder sich auf das Gebiet der höheren Mathematik mit entsprechend anspruchsvolleren Programmen zu begeben. Während die einfachen Ansätze eben auch einfach zu verstehen sind, führen die komplexeren Ansätze meist schneller zum Ziel. Wir beschränken uns hier auf einen langsam aber gut zu verstehenden Ansatz.
Dabei berücksichtigen wir den Umstand, dass die Entfernung von Punkten zueinander die zentrale Rolle spielt. Dazu erzeugen wir erst einmal eine Reihe von Punkten. Damir wir später unkompliziert auf diese zugreifen werden, soll jeder Punkt durch ein Objekt (einen Klon) dargestellt werden. Zuerst legen wir aber einige Variablen fest, damit wir unser Programm später möglichst flexibel verwenden können.
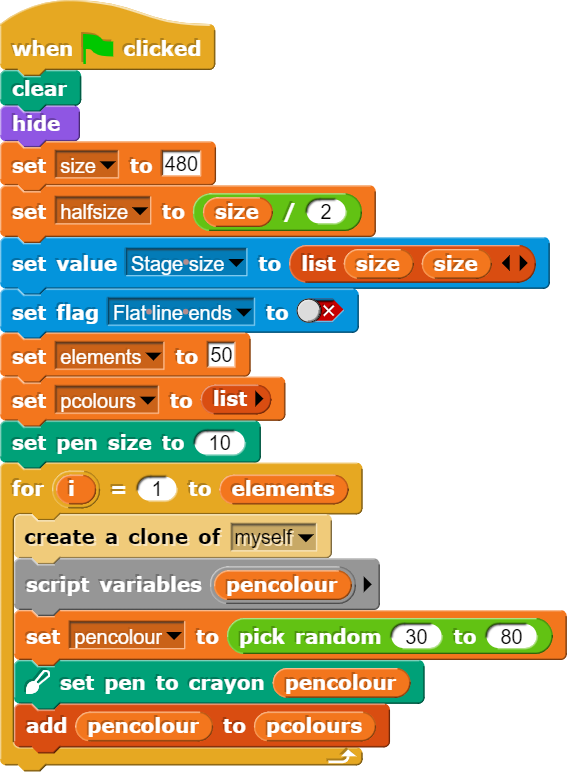
Am Anfang sorgen wir dafür, dass der Bildschirm leer ist und die gewünschte Auflösung aufweist. Dann erzeugen wir in einer for-Schleife die vorher festgelegte Anzahl von Klonen. Zusätzlich speichern wir ein einer Liste Farbwerte ab, mit denen wir einzelne Punkte einfärben und auf die wir dann später zugreifen können.

Sobald ein neuer Klon erzeugt wird, tritt dieser in Aktion: Der Klon springt an eine beliebige Stelle auf dem Bildschirm und zeichnet dort einen Punkt in der zuvor zugeordneten Farbe. Diese Punkte dienen uns als Startbedingungen für unsere Voronoi-Diagramme.
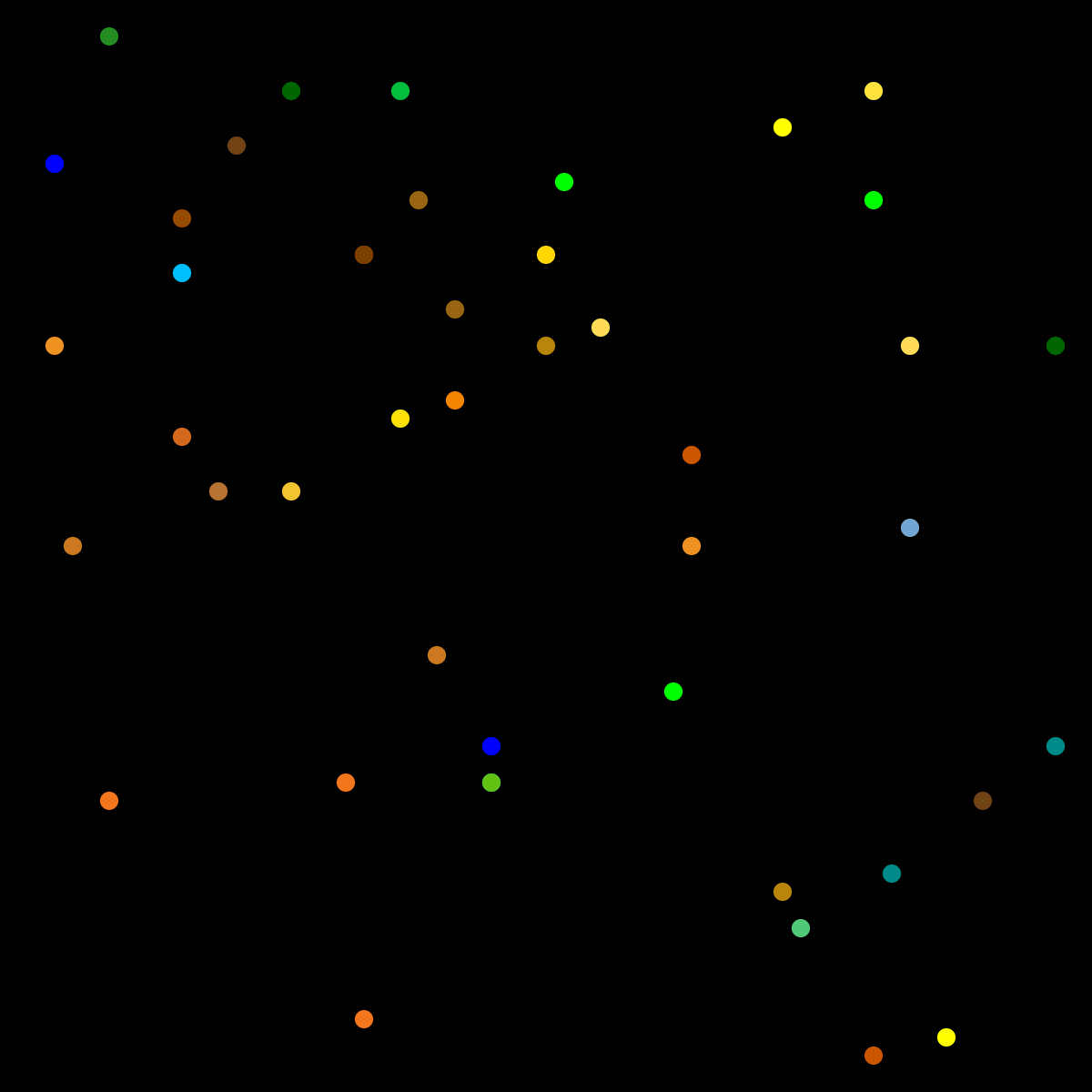
Im nächsten Schritt setzen wir nun den eigentlichen Algorithmus um, indem wir alle relevanten Orte des Bildes durchlaufen und dann jeweils schauen, welcher der farbigen Punkte am nächsten liegt. Konzentrieren wir uns erst einmal darauf, für einen Punkt auf dem Bildschirm den nächsten eingefärbten Punkt zu finden.
Mit dem folgenden Block können wir die Entfernung zwischen unserem festgelegten Bildschirmpunkt und allen vorher bestimmten Farbpunkten berechnen.

Das Ergebnis ist eine mehr oder weniger lange Liste von Entfernungen.
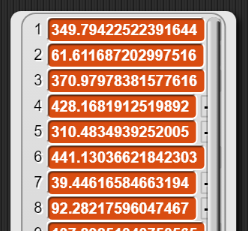
In einem nächsten Schritt kombinieren wir diese Liste von Entfernungen mit der bereits bestehenden Liste der Farbwerte für unsere Punkte und sortieren die so erhaltene Tabelle nach der kleinsten Entfernung.
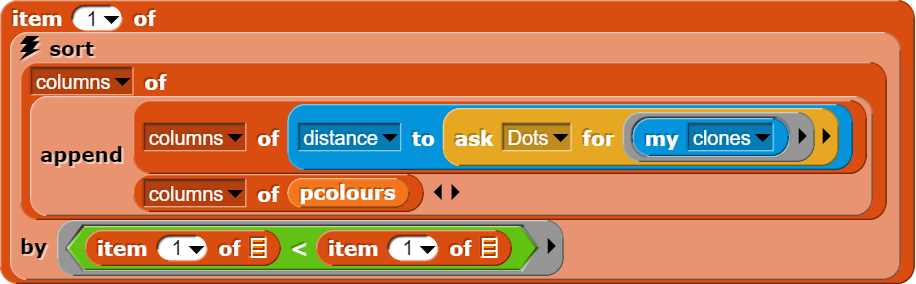
Damit erhalten wir die aktuelle Entfernung zum nächsten Farbpunkt und dessen Farbe. Diese Informationen nutzen wir nun, um die Bildschirmkoordinate entsprechend einzufärben. Im einfachsten Fall verwenden wir dazu einfach die Farbe, die wir ausgelesen haben, wodurch die Einzugsgebiete der einzelnen Farbpunkte sichtbar werden.

Da diese Berechnung ziemlich lange dauert, können wir die Schrittweise in der for-Schleife erhöhen und so erst einmal ein Vorschaubild erzeugen. Da dieses aber eher langweilig aussieht, nehmen wir gleich noch weitere Änderungen vor und zeichnen keine Quadrate, sondern Kreise deren Grösse und Transparenz von der Entfernung zum nächsten Punkt abhängig sind.

Damit erhalten wir ein Kunstwerk, welches fast den Anschein erweckt, wir hätten ein 3D-Bild berechnet. Dabei ist die Ausprägung der "Krümmung" davon abhängig, wie stark wir die Transparenz ändern. Grösse Werte führen zu flachen Bildern, kleine Werte zu starken Transparenzveränderungen, wobei der Effekt auch von der Auflösung des Ausgabebildschirms abhängig ist, da ja die Entfernung in Pixeln als Grundlage verwendet wird.
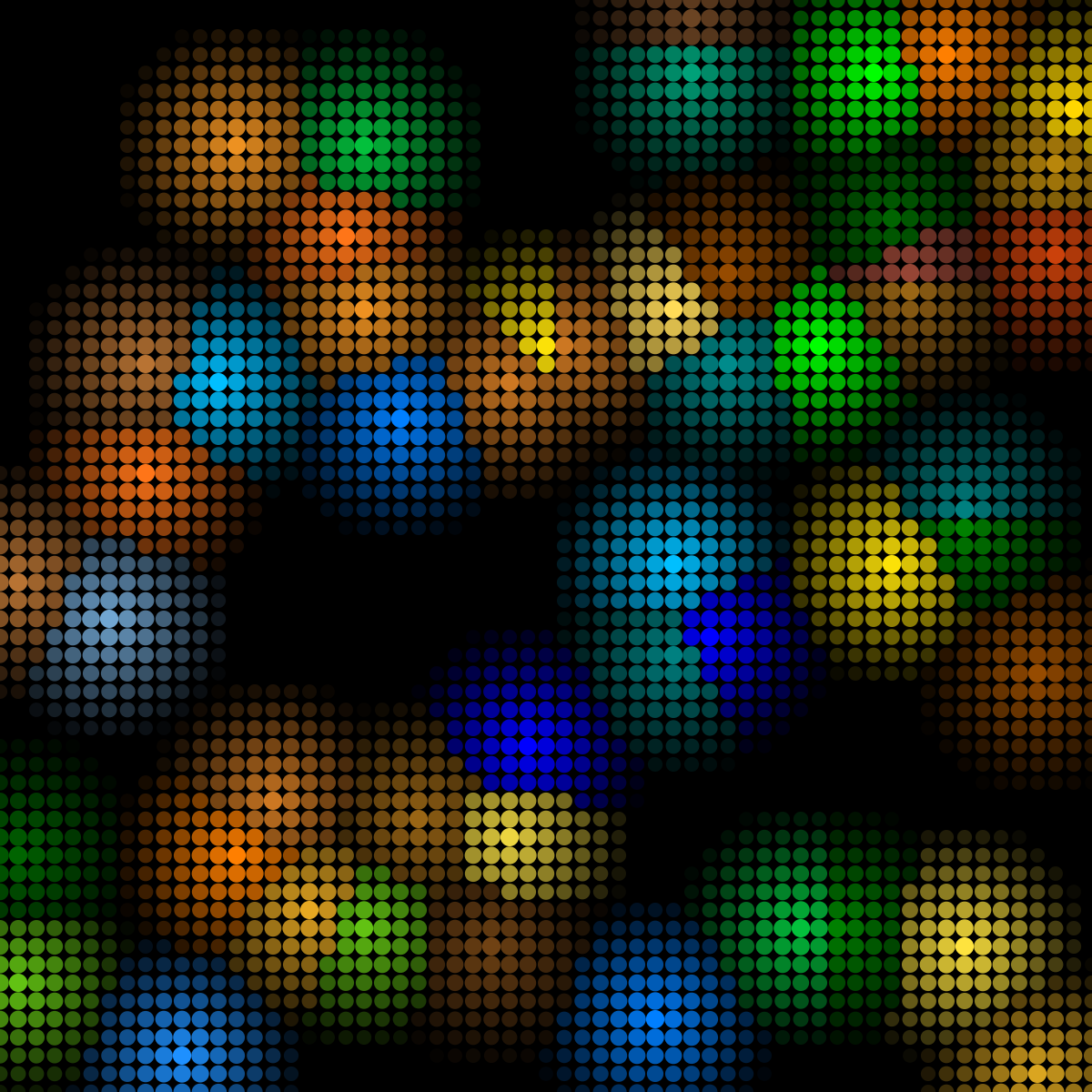
Wenn wir den Wert für die Transparenz invertieren, d.h. kleine Entfernungen sollen zu grosser Transparenz führen, erhalten wir ein Bild mit "Löchern".


Noch interessanter wird es, wenn wir diese Farbwerte mithilfe einer Modulusberechnung sich zyklisch wiederholen lassen. Damit können wir sozusagen Ringe um die Zentren anzeigen lassen, die wie durch Tropfen erzeugte Wellen auf einer Wasseroberfläche wirken. Hier lohnt es sich auf jeden Fall, mit den entsprechenden Einstellungen herumzuspielen.
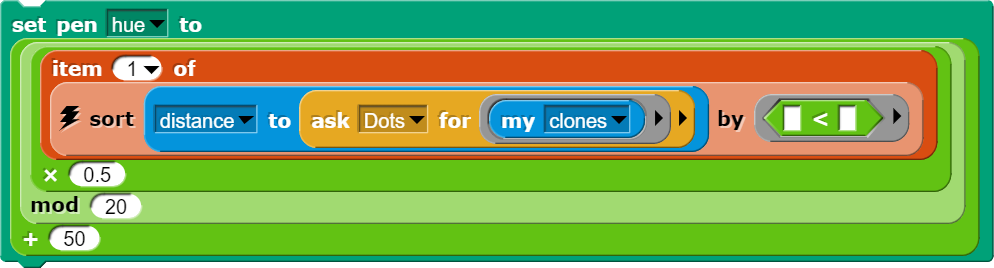
Für das Bild wurde eine Berechnung mit Modulus 10 verwendet, weil dadurch die konzentrischen Kreise etwas näher zusammenrücken.

Eine letzte Form von Voronoi-Diagramm erhalten wir, wenn wir statt des Farbwertes die Richtung zum Zentrum berücksichtigen und aus einem Raster heraus Schritte in diese Richtung unternehmen. Dann entstehen noch einmal ganz neue Strukturen.
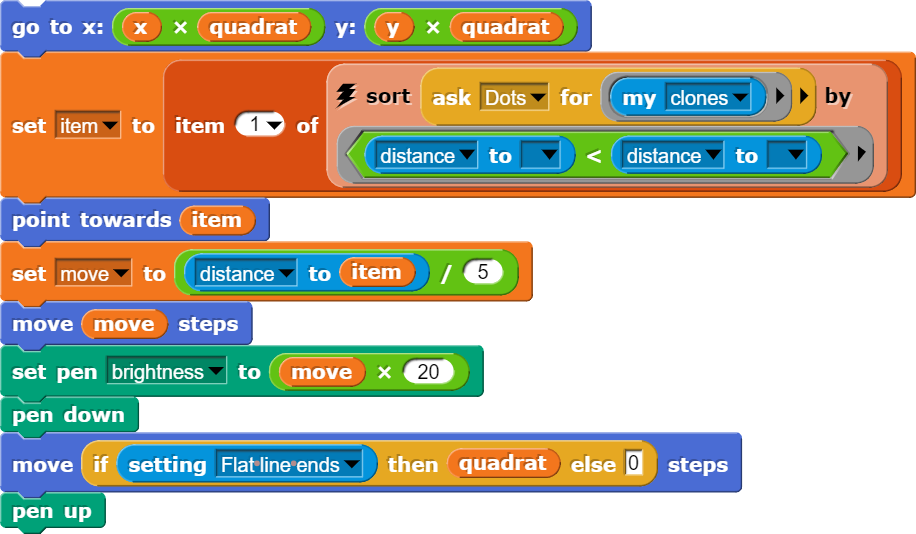
Die Breite der schwarzen Strassen zwischen den "Grasbüscheln" hängt davon ab, wie gross der Teiler gewählt wird. Je grösser der Teiler, desto schmaler die nicht eingefärbten Bereiche.

Du hast nun einige Beispiele gesehen, wie man die unterschiedlichen Informationen in ein Kunstwerk umwandeln kann. Nun bist du an der Reihe. Experimentiere mit verschiedenen Einstellungen oder schreibe Teile des Programms um. Erzeuge damit ein möglichst interessantes Kunstwerk und lade dieses zusammen mit einer Beschreibung, wie du vorgegangen bist, in die Galerie "Voronoi" hoch.
Das Programm selbst kannst du direkt hier aufrufen: Voronoi - Version 3.